PoPL Lecture 6

Agenda: Syntax (Co-inductive Terms)

• Last time, we had terms, defined in terms of induction and expression:
  • Defining a base case for an expression
  • Inductively, defining the set of all expressions
  • This was done for an operation
  • Example from last class

      |--------------------|           |
      | if n ∈  N          | num rule  |
      | ⇒ n AST            |           |  Defines all
      |         OR         |            > expressions
      | if e1 AST & e2 AST | plus rule |  in addition
      | ⇒ + e1 e2 AST      |           |
      |--------------------|           |
    

• This time, we will focus on Structural Induction: on trees, instead of $n$

Generalising induction

• We want to define terms inductively. Inductive terms
• We assume an alphabet $\Sigma$ of constructor symbols
  • What are constructor symbols? Kind of like functions that operate on some terms (arity, as we shall find out) and return terms as results. Think of the ‘+’ operator.
  • Eg: $\Sigma = {f, g, a, b}$
• We define an “arity” function that operates on $\alpha : \Sigma \to N$ (Natural numbers)
  • Arity defines how many parameters the operator can take.
  • Eg: $\alpha (f) = 2, \alpha (g) = 1, \alpha (a) = \alpha (b) = 0$
• So, terms can be built like:

  f(a(), b()) \_ inductively building terms
  f(g(a), b)  /
  

• So, to define inductive terms: Given a constructor symbol f with arity α(f) = n and n terms, f(the n terms) = a new term

  t₁ ... n terms  and α(f) = n     \
  ----------------------------      > constructor rule
  ⇒ f(t₁ ... n terms) is a term    /
  

• Can be used to make judgements on terms (slide below)

  

• wordy definition of this:
  • if $t_1 … t_n$ Terms
  • and $f \in \Sigma$ s.t. $\alpha(f) = n$
  • then $f(t_1 … t_n)$ is a term

• The set of all Inductive terms over $\Sigma \implies T_{ind}(\Sigma)$ is the smallest set satisfying the above properties:

  So Tᵢₙ∑ would have: 
    a, b, f a b, g a, g b, f g a b, f a g b, 
    g f a b, f g f a b a, etc
  

• Why bother with a boring induction based proof? We will move on to eventually define evaluation itself as an induction system, not just terms.

  

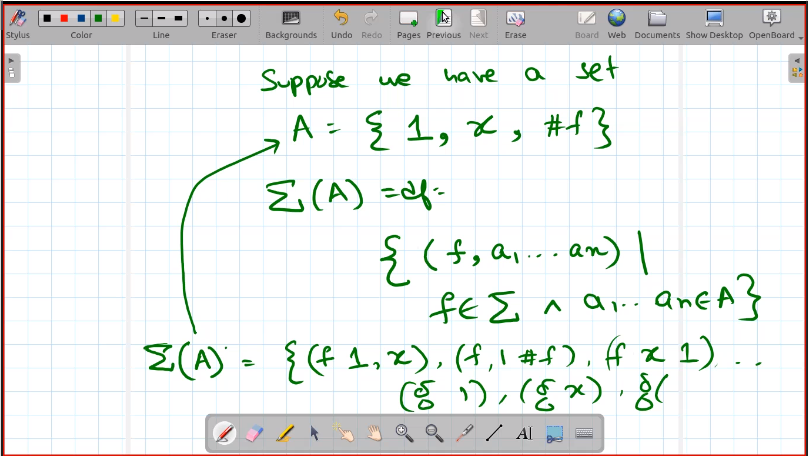
• What is a set $X = \Sigma(X)$. We need the least solution, as there are many.

$T_{ind}$ is the least solution.

Saying that this is the least solution and giving the definition of it is identical.

• Is it possible to have ‘infinite’ terms?

We have                  Can we have
          +                          g
         / \                        / 
        a   b                      g'    or  g<-\
                                  /          |__| 
                                 g''
        

• Any proof is a finite structure
• The set itself is infinite
• But every element in the set if finitely constructed
• $T_{ind} = \Sigma(T_{ind}) \subset T_{ind}$
• Testing a $\sum$ operator
• Hey ~a\ cat~
• [This is in small caps]{.smallcaps}